



Next: �褤���Ȥϲ���?
Up: ��������ο���Ū�����դ�
Previous: ��������ο���Ū�����դ�
�����k�ӥå���Υ֥��å��˶��ڤ�, �֥��å������沽������������֥��å���椬����Ū�ˤɤ����Ҥ���뤫, �����ƤɤΤ褦����������Ĥ���ͤ��Ƥߤ褦.
B��0��1����Ĥθ�����ʤ뽸��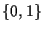 �Ȥ����, 0��1����ʤ�k�ӥåȤο������Τ�B��k�Ĥ�ľ��Bk��Ʊ���Ǥ���.
�Ȥ����, 0��1����ʤ�k�ӥåȤο������Τ�B��k�Ĥ�ľ��Bk��Ʊ���Ǥ���.
�������Ĥ��ĤФ餷�Ƴ�̤����줿�����Ȼפ������Τ�ʤ���, �����̤�Ǥ���.
����, �������뤳�Ȥ�, ���Τ褦�ʡֿ��ء�Ūɽ������ǽ�ˤʤ�ΤǤ���.
��k�ӥåȤο����l�ӥåȤ�;ʬ�ʾ�����ղä�������֥��å�����ͤ��뤳�Ȥˤ����, ������沽�ϼ��Τ褦�˥�ǥ벽�����.
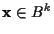 ����,
����,
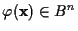 ��
x����沽���줿��ΤȤ����櫓�Ǥ���(ñ�ͤȤ�����郎ɬ�פʤΤ�, �㤦�ǡ�������沽����Ʊ����ΤˤʤäƤ�, ���椬�Ǥ��ʤ��ʤ뤫��Ǥ���).
���Τ褦�˥�ǥ벽�����֥��å����ˤĤ���,
k������Ĺ(information length),
n�����Ĺ(code length),
n-k������(redundancy),
k/n����沽Ψ(infomation rate, �ޤ��� code rate)�Ȥ���,
���Ĺn, ����Ĺk������(n,k)-���Ȥ���.
�ޤ�, ñ��
��
x����沽���줿��ΤȤ����櫓�Ǥ���(ñ�ͤȤ�����郎ɬ�פʤΤ�, �㤦�ǡ�������沽����Ʊ����ΤˤʤäƤ�, ���椬�Ǥ��ʤ��ʤ뤫��Ǥ���).
���Τ褦�˥�ǥ벽�����֥��å����ˤĤ���,
k������Ĺ(information length),
n�����Ĺ(code length),
n-k������(redundancy),
k/n����沽Ψ(infomation rate, �ޤ��� code rate)�Ȥ���,
���Ĺn, ����Ĺk������(n,k)-���Ȥ���.
�ޤ�, ñ��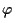 �ˤ��Bk����
�ˤ��Bk����
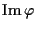 �����(code)�Ȥ���,
�����(code)�Ȥ���,
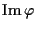 �θ��������Ȥ���.
�ʲ�,
�θ��������Ȥ���.
�ʲ�,
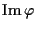 ��C�Ƚ��Ȥˤ���.
��C�Ƚ��Ȥˤ���.
| �Ѹ�ΤޤȤ� |
| ���Š|
= |
���Υӥåȿ� |
| ����Š|
= |
����ӥåȤ�Ĺ�� |
| ���� |
= |
���Ĺ-����Ĺ |
| ��沽Ψ |
= |
���������Š|
���� 4.2
��
![[*]](/icons/cross_ref_motif.gif)
, ��
![[*]](/icons/cross_ref_motif.gif)
�����ˤĤ���,
���Ĺ, ����Ĺ, ��Ĺ��, ��沽Ψ����Ƥߤ褦.
�ʾ�ε���β���, �֥��å����θ��������ˤĤ��ƹͤ��Ƥߤ褦.���Τ����, �ޤ��ϥߥ�Υ�Ȥ�����ǰ��Ƴ������.
��� 4.3
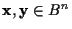
����,
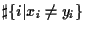
(���ʤ���ۤʤ���ʬ�θĿ�)
��
x��
y��
�ϥߥ�Υ�Ȥ���,
d(
x,
y)��ɽ��. ����ϵ�Υ�θ�����������
![[*]](/icons/foot_motif.gif)
.
�� 4.4
�㤨��, n=4�ξ��,
d((0,0,0,0), (0,0,0,1))=1,
d((0,1,0,1), (1,1,0,0))=2�ʤɤȤȤʤ�.
����, ����
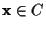 ����������, �����꤬�������������줬
x'���ä��Ȥ���Ȥ�,
����������, �����꤬�������������줬
x'���ä��Ȥ���Ȥ�,
�Ǥ��뤫��,
���Υϥߥ�Υ��Ȥ���,
��ɽ������뤳�Ȥ�ʬ����.
�����̿���Ԥä�, ����¦��
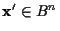 �Ȥ���������������ä��Ȥ���. ����¦�����������줬���Ǥ��ä����Τ�褷��ʤ�����, �����줫������������Ƥ�(��������)���Ȥ�ɬ�פȤʤ�. ����ˤϤɤ�����Ф褤����������
�Ȥ���������������ä��Ȥ���. ����¦�����������줬���Ǥ��ä����Τ�褷��ʤ�����, �����줫������������Ƥ�(��������)���Ȥ�ɬ�פȤʤ�. ����ˤϤɤ�����Ф褤����������
����, �ƥӥåȤ��Ф���, ���꤬�������Ψ���ɤ����������Ω��p�Ǥ���Ȥ��褦(2���о��̿�ϩ). p���̿�ϩ�Υϡ���Ū������������ޤ����˾��������Ǥ��뤬(�Ȥ�������ʬ�������ʤ���п��ѤΤ������̿�ϩ�Ȥʤ�ʤ�), �����Ǥ��ص���p=10-a, (a>1)�ȤǤ⤷�Ƥ�����. �����,
x���̿���Υ��顼��
y�ˤʤ��Ψ
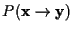 ��,
��,
�Ȥʤ뤫��,
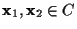 ������,
������,
�Ǥ���,
x'�˥ϥߥ�Υ�Ƕᤤ���֤ˤ����Τۤ�
x'��������Ǥ����Ψ���⤤(�Ϻ��ǤϤʤ�����Ū�˹⤤)���Ȥ�ʬ����.
�������ä�, �Ǥ⸶��Ū�ʸ�����������ˡ�Ȥ���,
x'�ȤΥϥߥ�Υ�����־�����C�θ�����������ȡֻפ���(�����ϥ���Ƥ��뤳�Ȥ⤢��)�Ȥ�������ˡ���ͤ�����Ǥ�����. �������������(�Ǥ����餷����Τ����Ȥ�����̣)�Ȥ���.
����Ǥ��٤Ƥ���꤯�����Ф褤�Τ���, ��ǰ�ʤ����������ˤϼ��Τ褦�ʼ���������.
- 1.
- C�θ������������Ĵ�٤�Τ�, ���Ȥ��äƤ���֤�������.
- 2.
- ���ֶᤤ�Ȥ����ˤ����Τ���Ĥ����Ȥϸ¤�ʤ�.
�������ä�����������������椬, ������Ҥ٤�Ǿ���Υ����Ǥ���.
������������뤿���, �����̤�����ˤʤ�.
��� 4.5
���
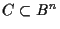
����,
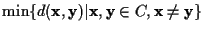
��
C��
�Ǿ���Υ�Ȥ���,
d(
C)�ޤ���, ñ��
d�Ƚ�.
�ޤ�, �Ǿ���Υ��
d��(
n,
k)-����(
n,
k,
d)-���Ȥ���.
������
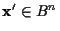 ������,
������,
�Ȥ��������ͤ���. �����, d��C�κǾ���Υ�Ǥ��뤳�Ȥ���,
Ǥ�դ�
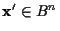 ������,
������,
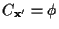 ���ޤ���
Cx'��ͣ��Ĥθ�����ʤ�. ���ΤȤ�, ������
���ޤ���
Cx'��ͣ��Ĥθ�����ʤ�. ���ΤȤ�, ������
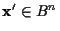 ������,
������,
�ˤ�äƼ����줫��θ���������Ԥ�����ˡ���Ǿ���Υ�����Ȥ���(������).
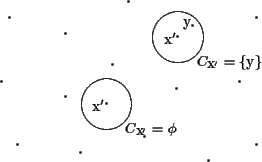
�Ǿ���Υ������Ѥ������������ˤ����Ƥ�, ������������������,
ͣ��Ĥ�C�θ��ؤ����椵���. ����θ����ϥߥ�Υ��d/2̤����
���֤ˤ����Τ˹ʤ뤳�Ȥ�, ������֤�����, �ޤ�Ʊ����, ����Ǥ���
���ˤ�ͣ��Ĥ���ޤ뤳�Ȥ��ݾڤ���뤳�Ȥˤʤ�. ����Ǥ��ʤ�����
�����ʤ�Ƥ����ø��ʤ��ȤǤɤʤ�����ͤ�, ��ʰ�����������
�����������, ����Ǥ��ʤ�����, �������᤹��ʤ겿�ʤ��̤���ˡ��
�Τ�Ф褤�����Τ��ȤǤ���. �ʸ�, �ܹƤǤ�, �Ǿ���Υ����Τߤ�ͤ��뤳�Ȥˤ���
![[*]](/icons/foot_motif.gif) .
.
���� 4.6
��������, �Ǿ���Υ����Ȥ��, ��������ǽ�Ϥ˴ؤ��Ƥ�,
Bn���
C�����λ���Ф���(�ߤ���Υ��Ƥ���Ф���ۤɤ褤)�Τߤ˰�¸��, ��ñ��
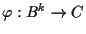
��������ˤ�̵�ط��Ǥ��뤳�Ȥ����դ��Ƥ�����. �������,
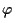
����沽������Υץ�������ô������ʼ����ǤϤ��뤬, ����, �����������Ȥ�, ���Ф���
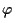
�Τ��Ȥ�˺���
C�Τߤ�ͤ��뤳�Ȥˤʤ�.




Next: �褤���Ȥϲ���?
Up: ��������ο���Ū�����դ�
Previous: ��������ο���Ū�����դ�
Mitsuru Kawazoe
2001-11-14
![]() �Ȥ����, 0��1����ʤ�k�ӥåȤο������Τ�B��k�Ĥ�ľ��Bk��Ʊ���Ǥ���.
�Ȥ����, 0��1����ʤ�k�ӥåȤο������Τ�B��k�Ĥ�ľ��Bk��Ʊ���Ǥ���.

![]() ����������, �����꤬�������������줬
x'���ä��Ȥ���Ȥ�,
����������, �����꤬�������������줬
x'���ä��Ȥ���Ȥ�,
![]() �Ȥ���������������ä��Ȥ���. ����¦�����������줬���Ǥ��ä����Τ�褷��ʤ�����, �����줫������������Ƥ�(��������)���Ȥ�ɬ�פȤʤ�. ����ˤϤɤ�����Ф褤����������
�Ȥ���������������ä��Ȥ���. ����¦�����������줬���Ǥ��ä����Τ�褷��ʤ�����, �����줫������������Ƥ�(��������)���Ȥ�ɬ�פȤʤ�. ����ˤϤɤ�����Ф褤����������
![]() ��,
��,
![]() ������,
������,
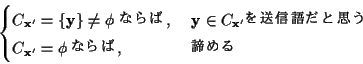
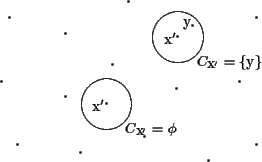
![]() .
.