



Next: 線形符号の基礎
Up: 線形符号
Previous: 線形符号
元のデータの形式はいろいろだが, 通信に使われるデータは, 結局のところ,
1 と 0 からなる数字の列にほかならないってことで, 前章では,
0 と 1 だけからなる数の集合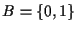 を考えたわけだが, ここでは, さらに
この集合Bに,
足し算, 引き算, かけ算, 割算の四則演算の入れたものを考える.
ここでの, 足し算, 引き算, かけ算, 割り算で, 普通と違うのは次の一点だけである.
を考えたわけだが, ここでは, さらに
この集合Bに,
足し算, 引き算, かけ算, 割算の四則演算の入れたものを考える.
ここでの, 足し算, 引き算, かけ算, 割り算で, 普通と違うのは次の一点だけである.
1+1=0
これは, 1+1がBからはみ出すことを防ぐためのものである.
これさえつけておけば, Bが四則演算について閉じていることが保証される.
あれ? 0-1=-1は? と思う人がいるかも知れない.
これは 1+1=0より, 1=-1となるから大丈夫なのだ.
この四則演算の入ったBは数学で体と呼ばれるものになり,
通常 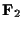 という記号で書かれる.
という記号で書かれる.
で, この 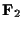 をBの代わりに使うと, どうなるか.
まず,
をBの代わりに使うと, どうなるか.
まず,
となることは, Bのときと同様.
3ビットのときの例も見た目はBと全く変わらない.
じゃあ, Bのときと何がちがうねん, という声が聞こえてきそうだが,
ここで, 思い出して欲しい, 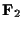 には四則演算が入っていることを.
この四則演算を使って,
には四則演算が入っていることを.
この四則演算を使って,
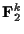 にはベクトルの足し算や
にはベクトルの足し算や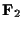 の元によるスカラー倍
(実際には「1倍」と「0倍」しかないのだが)が定義される.
の元によるスカラー倍
(実際には「1倍」と「0倍」しかないのだが)が定義される.
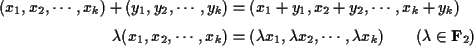
すなわち,
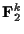 は
は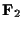 上の線形空間(ベクトル空間)
上の線形空間(ベクトル空間)
![[*]](/icons/foot_motif.gif) というわけだ. で, 線形空間として見ることには次の利点がある.
というわけだ. で, 線形空間として見ることには次の利点がある.
5桁の符号語01000を送ったらエラーが起こって, 01001になったとしよう.
このときエラーは3番目と5番目のビットに起こったわけだが, ベクトル表記を用いると,
x=(0,1,0,0,0),
y=(0,1,0,0,1)としたとき,
と書け,
eの0でない成分のある場所がエラーの起こった個所を示すことになる. このように, 送信語と受信語そしてエラーの関係をベクトルの足し算を用いることにより, 分かりやすく記述することができるのが線形空間を用いる大きな利点の一つである.
上のように, 送信語
xと受信語
yに対し,
y=x+eとなる
ベクトル
eのことを誤りベクトルと呼ぶ.
この利点を生かすべく, ブロック符号の数学的定式化として用いた集合の間の単射
の代わりに, 1対1の線形写像
を用いる. このように,
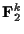 から
から
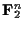 (n>k)への1対1線形写像の像となっているような特別なブロック符号を線形符号とよぶ.
(n>k)への1対1線形写像の像となっているような特別なブロック符号を線形符号とよぶ.
注意 1.1
一応注意しておくと,
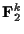
から
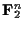
(
n>
k)への1対1線形写像の像は
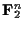
内の
k-次元部分空間を定め, 逆に,
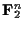
内の
k-次元部分空間に
対して,
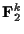
からの同型写像(したがって当然1対1)が存在するから, 結局,
線形符号とは
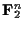
内の
k-次元部分空間である, といっても同じことにある.
以下, 本稿では線形符号のみを考える.
線形符号が一般の符号の中でよいものであるという理由については次節で述べる.
Mitsuru Kawazoe
2001-11-14
![]() を考えたわけだが, ここでは, さらに
この集合Bに,
足し算, 引き算, かけ算, 割算の四則演算の入れたものを考える.
ここでの, 足し算, 引き算, かけ算, 割り算で, 普通と違うのは次の一点だけである.
を考えたわけだが, ここでは, さらに
この集合Bに,
足し算, 引き算, かけ算, 割算の四則演算の入れたものを考える.
ここでの, 足し算, 引き算, かけ算, 割り算で, 普通と違うのは次の一点だけである.
![]() をBの代わりに使うと, どうなるか.
まず,
をBの代わりに使うと, どうなるか.
まず,
