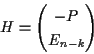Next: 双対符号
Up: 線形符号の基礎
Previous: 線形符号の代数的表現(1)
さて, 上で見てきたのは, 線形符号を定義通り
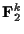 から
から
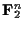 への1対1の線形写像の像としてみることだったが, 実はもう一つ別の見方がある.
への1対1の線形写像の像としてみることだったが, 実はもう一つ別の見方がある.
(n,k)-線形符号
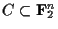 は,
は,
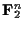 のk-次元線形部分空間であるから,
のk-次元線形部分空間であるから,
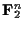 から
から
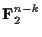 への線形写像でCを核(kernel)とするものが存在する. この写像を
への線形写像でCを核(kernel)とするものが存在する. この写像を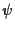 とすると,
とすると,
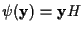 となるような行列
となるような行列
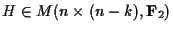 が存在する.
が存在する.
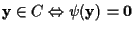 であるから,
であるから,
が成り立つ. したがって, 線形符号Cは, 斉次連立一次方程式
yH=の解空間として捉えられることがわかる. このHをCのパリティ検査行列(parity check matrix)と呼ぶ.
簡単にわかることだが, 線形符号Cの生成行列が標準形(Ek P)であるとき, パリティ検査行列Hは,
で与えられる.
Mitsuru Kawazoe
2001-11-14
![]() から
から
![]() への1対1の線形写像の像としてみることだったが, 実はもう一つ別の見方がある.
への1対1の線形写像の像としてみることだったが, 実はもう一つ別の見方がある.
![]() は,
は,
![]() のk-次元線形部分空間であるから,
のk-次元線形部分空間であるから,
![]() から
から
![]() への線形写像でCを核(kernel)とするものが存在する. この写像を
への線形写像でCを核(kernel)とするものが存在する. この写像を![]() とすると,
とすると,
![]() となるような行列
となるような行列
![]() が存在する.
が存在する.
![]() であるから,
であるから,