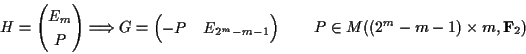
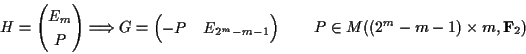
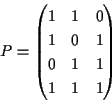
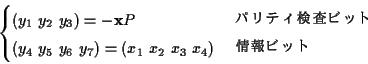
| Њр у•”•√•» | •—•к•∆•£Є°ЇЇ•”•√•» | Њр у•”•√•» | •—•к•∆•£Є°ЇЇ•”•√•» |
| (0,0,0,0) | (0,0,0) | (1,0,0,0) | (1,1,0) |
| (0,0,0,1) | (1,1,1) | (1,0,0,1) | (0,0,1) |
| (0,0,1,0) | (0,1,1) | (1,0,1,0) | (1,0,1) |
| (0,0,1,1) | (1,0,0) | (1,0,1,1) | (0,1,0) |
| (0,1,0,0) | (1,0,1) | (1,1,0,0) | (0,1,1) |
| (0,1,0,1) | (0,1,0) | (1,1,0,1) | (1,0,0) |
| (0,1,1,0) | (1,1,0) | (1,1,1,0) | (0,0,0) |
| (0,1,1,1) | (0,0,1) | (1,1,1,1) | (1,1,1) |