



Next: 巡回符号の生成行列
Up: 巡回符号
Previous: 巡回符号の定義
巡回符号は多項式環の言葉で表現することができる.
![$\sigma : {\bf F}_2^n\to{\bf F}_2[X]/(X^n-1)$](img112.gif) を
を
で定義される線形写像とすると, これは同型写像となる.
これによって, まず,
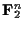 と
と
![${\bf F}_2[X]/(X^n-1)$](img114.gif) を同一視する.
を同一視する.
この同一視において,
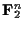 での作用Sは,
での作用Sは,
![${\bf F}_2[X]/(X^n-1)$](img114.gif) の方では
「Xをかける」ということに相当する. つまり,
の方では
「Xをかける」ということに相当する. つまり,
が可換(Sをやってから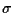 で移すのと,
で移すのと, 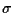 で移してからXをかけるのとでは結果は同じ)ということである.
ちょっと確認してみよう.
で移してからXをかけるのとでは結果は同じ)ということである.
ちょっと確認してみよう.
ほらね.
上の同一視のもとで, 巡回符号について次のことが成り立つ.
補題 2.1
上の
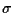
による巡回符号
Cの像
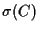
は
![${\bf F}_2[X]/(X^n-1)$](img114.gif)
のイデアルである.
![\begin{proof}[【証明】]
\par$\sigma({\mathbf a}),\sigma({\mathbf b})\in \sigma(C...
...athbf a})=\sum_{i=0}^{n-1}b_i(X^i\sigma({\mathbf a}))\in\sigma(C)$ .
\end{proof}](img119.gif)
この補題から,
となる.
したがって, 今後はイデアルの性質を調べていくことになるが, その前に,
多項式環のイデアルについての重要な事実を述べておこう.
補題 2.2
![${\bf F}_2[X]/(X^n-1)$](img114.gif)
は主イデアル環,
つまり, すべてのイデアルは唯一つの元から生成される.
![\begin{proof}[{\bf 証明}]
$I$ を$(0)\not=I\subsetneq{\bf F}_2[X]/(X^n-1)$ なるイ...
...)g(X)\in I\end{displaymath}より,
$r(X)\equiv 0$ でなければならない.
\end{proof}](img121.gif)
この事実から, (n,k)-巡回符号は次のように表現されることがわかる.
ただし, g(X), q(X)は,
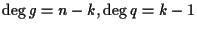 なる多項式である.
なる多項式である.
Mitsuru Kawazoe
2001-11-14
![\begin{displaymath}{\bf F}_2^n\ni{\mathbf a}=(a_1,a_2,\dots,a_n)
\longmapsto
\sum^n_{i=1}a_iX^{i-1}\in {\bf F}_2[X]/(X^n-1)
\end{displaymath}](img113.gif)
![\begin{displaymath}{\bf F}_2^n\ni{\mathbf a}=(a_1,a_2,\dots,a_n)
\longmapsto
\sum^n_{i=1}a_iX^{i-1}\in {\bf F}_2[X]/(X^n-1)
\end{displaymath}](img113.gif)
![]() での作用Sは,
での作用Sは,
![]() の方では
「Xをかける」ということに相当する. つまり,
の方では
「Xをかける」ということに相当する. つまり,
![\begin{displaymath}\begin{CD}
{\bf F}_2^n @>{\sigma}>> {\bf F}_2[X]/(X^n-1) \\
...
...ot}V \\
{\bf F}_2^n @>{\sigma}>> {\bf F}_2[X]/(X^n-1)
\end{CD}\end{displaymath}](img115.gif)
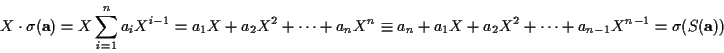
![\begin{proof}[【証明】]
\par$\sigma({\mathbf a}),\sigma({\mathbf b})\in \sigma(C...
...athbf a})=\sum_{i=0}^{n-1}b_i(X^i\sigma({\mathbf a}))\in\sigma(C)$ .
\end{proof}](img119.gif)
![\begin{proof}[{\bf 証明}]
$I$ を$(0)\not=I\subsetneq{\bf F}_2[X]/(X^n-1)$ なるイ...
...)g(X)\in I\end{displaymath}より,
$r(X)\equiv 0$ でなければならない.
\end{proof}](img121.gif)
![\begin{displaymath}\begin{CD}
{\bf F}_2^n @>{\cong}>> {\bf F}_2[X]/(X^n-1) @.\\...
...)=(g(X))@.=\{q(X)g(X) \vert \deg q(X)\le n-1-\deg g\}
\end{CD}\end{displaymath}](img122.gif)