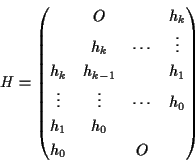Next: 巡回符号の最小距離
Up: 巡回符号
Previous: 巡回符号の生成行列
今度は, パリティ検査行列を求めてみよう.
g(X)h(X)=Xn-1
なる
![$h(X)\in{\bf F}_2[X]$](img131.gif) ,
,
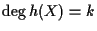 をとると,
をとると,
に対して,
ここで,
である. なぜなら,
ならば,
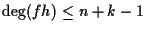 より,
より,
の次数は, k-1 以下. 一方,
h(X) | gcd(f(X)h(X),Xn-1)
より, 結局,
となるからである.
よって,
とすると,
となる.
このTHの表現行列Hは, 簡単な計算で,
となることがわかる.
問題 4.1
前節で求めた生成行列Gと上で求めたパリティ検査行列Hの積GHが
零行列になることを確かめよ.
Mitsuru Kawazoe
2001-11-14