Next: 拡大体上の符号とバースト誤り
Up: BCH code
Previous: BCH code
符号長nが奇数であるような巡回符号のパリティ検査行列について
前章とは別の視点から考察する.
前章で見たように, Cを(n,k)-巡回符号とすると,
![$C=(g(X))\subset {\bf F}_2[X]/(X^n-1)$](img149.gif) と書ける.
と書ける.
このとき,
が成り立つ.
とくに
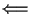 は, nが奇数のときXn-1が重根を持たない
ことから従う.
は, nが奇数のときXn-1が重根を持たない
ことから従う.
 と書き表したとき,
と書き表したとき,
と書ける.
g(X)の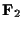 上での既約分解
(すなわち,
上での既約分解
(すなわち,
![${\bf F}_2[X]$](img154.gif) の既約元の積に書き表すこと)が,
の既約元の積に書き表すこと)が,
であるとき,
より,
となる.
ここで,
とおくと,
であることがわかる.
注意 1.1
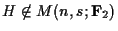
であることに注意.
例 1.2 (tex2html_wrap_inline$(7,4,3)$-ハミング符号)
X7-1=(X+1)(X3+X+1)(X3+X2+1)
このとき,
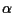
を
X3+
X+1の根(すなわち,
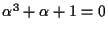
)
とすると,
![$f(X)=f_0+f_1X+\cdots+f_6X^6\in{\bf F}_2[X]/(X^7-1)$](img164.gif)
に対して,
が成り立つ. よって,
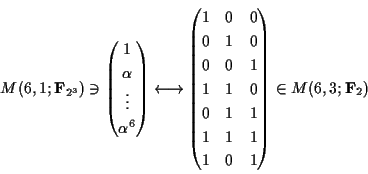
Cのパリティ検査行列は,
となる.
前章のパリティ検査行列との関係.
より,
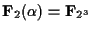 |
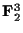 |
| 1 |
1 |
0 |
0 |
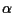 |
0 |
1 |
0 |
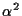 |
0 |
0 |
1 |
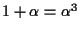 |
1 |
1 |
0 |
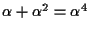 |
0 |
1 |
1 |
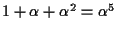 |
1 |
1 |
1 |
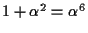 |
1 |
0 |
1 |
上の対応から,
送信語
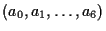 を送って,
を送って,
となったとすると,
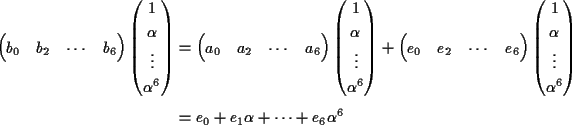
となる.
エラー個所が一ヵ所ならば, 唯一つの
iについてのみ
ei=1で,
他の
ejについては
ej=0となるから,
となることが分かる.
誤り訂正手順
- 1.
- 受信語
b=b(X)に対して,
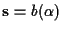 を計算,
を計算,
- 2.
-
s=ならば, 誤りなし,
- 3.
-
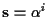 ならば,
b+ei,
ならば,
b+ei,
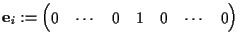 で誤り訂正.
で誤り訂正.
考察 1.3
前々章のハミング符号の誤り訂正アルゴリズムと比較せよ.




Next: 拡大体上の符号とバースト誤り
Up: BCH code
Previous: BCH code
Mitsuru Kawazoe
2001-11-14
![]() と書ける.
と書ける.
![]() と書き表したとき,
と書き表したとき,
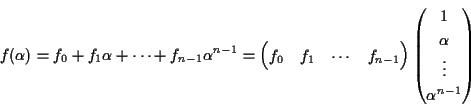
![]() 上での既約分解
(すなわち,
上での既約分解
(すなわち,
![]() の既約元の積に書き表すこと)が,
の既約元の積に書き表すこと)が,
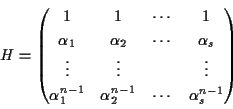
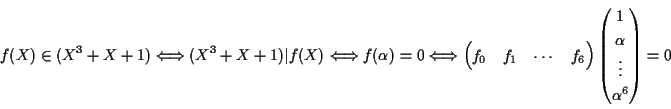
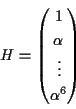
![]() を送って,
を送って,