



Next: Reed-Solomon code §ő∆√ńߧ»∑ÁŇņ
Up: Reed-Solomon code
Previous: ńÍĶŃ
(x,y)§ő∆Ī√Õőŗ§Ú(x:y)§»Ĺ٧Į§≥§»§ň§Ļ§Ž§»,
§»§Ļ§Ž§≥§»§ň§Ť§√§∆, 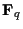 §Ō
§Ō
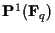 §ő…Ű ¨ĹłĻÁ§»§ §Í,
§ő…Ű ¨ĹłĻÁ§»§ §Í,
§»§ §Ž. §∑§Ņ§¨§√§∆,
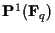 §Ō,
§Ō, 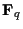 §ňŐĶł¬ĪůŇņ§Ú…’§Ī≤√§®§∆•≥•ů•—•Į•»≤ŧ∑§Ņ§Ť§¶§ §‚§ő§»Ľ◊§¶§≥§»§¨§«§≠§Ž( £Ń« ŅŐŐ§ő•≥•ů•—•Į•»≤ŧő•Ę• •Ū•ł°ľ). §≥§ő(1:0)§Ú
§ňŐĶł¬ĪůŇņ§Ú…’§Ī≤√§®§∆•≥•ů•—•Į•»≤ŧ∑§Ņ§Ť§¶§ §‚§ő§»Ľ◊§¶§≥§»§¨§«§≠§Ž( £Ń« ŅŐŐ§ő•≥•ů•—•Į•»≤ŧő•Ę• •Ū•ł°ľ). §≥§ő(1:0)§Ú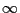 §»§ę§Į§≥§»§ň§Ļ§Ž.
§»§ę§Į§≥§»§ň§Ļ§Ž.
![\begin{align*}P_1, P_2, \cdots , &P_n , Q \in{\bf P}^1({\bf F}_q),
\quad P_i\n...
...Őį ≤ľ§ő∂ň§ÚĽż§ń${\bf P}^1$ 匧őÕ≠ÕżīōŅŰ}\}
= {\bf F}_q[x]_{<k} \\
\end{align*}](img211.gif)
§≥§¶§∑§∆īŲ≤Ņ≥ōŇ™§ §‚§ő§»§∑§∆§»§ť§®§∆§Ŗ§Ž§», …šĻś§ÚļÓ§Ž§»§§§¶ī—Ňņ§ő§Ŗ
§ę§ť§Ō, Pj §¨ł∂ĽŌq-1ĺŤļ¨§Ú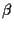 §»§∑§∆
§»§∑§∆
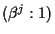 §«ÕŅ§®§ť§ž§Ž…¨Õ◊§Ō§ §Į, Pj=(x:1),
§«ÕŅ§®§ť§ž§Ž…¨Õ◊§Ō§ §Į, Pj=(x:1),
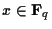 §«§Ę§ž§–§Ť§§
§»§§§®§Ž. (ļ«ĺģĶųő•§š…ŁĻś§ő∑◊ĽĽőŐ§Ō ŐŐš¬Í)
§«§Ę§ž§–§Ť§§
§»§§§®§Ž. (ļ«ĺģĶųő•§š…ŁĻś§ő∑◊ĽĽőŐ§Ō ŐŐš¬Í)
Mitsuru Kawazoe
2001-11-14
![]()