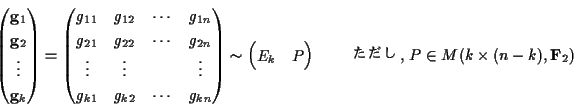Next: 線形符号の代数的表現(2)
Up: 線形符号の基礎
Previous: 線形符号の基礎
さて, これから少し線形代数のお話. 線形代数の本では, 大抵の場合, ベクトルといったら縦ベクトル(ようするに数字が縦に並んでいるやつね)で,
などと書かれるのが標準だが, 情報理論では, 前節で
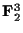 の元
x=(x1,x2,x3)を考えたように, 普通横ベクトルを使う(コンピュータが横書き文化だからだろうが, その方がイメージに合うのだ, なんとなく). したがって, 同じ線形代数でも普段見慣れているのとはちょっと見た目が異なることになる(外見が異なるだけで本質は何も変わらない).
の元
x=(x1,x2,x3)を考えたように, 普通横ベクトルを使う(コンピュータが横書き文化だからだろうが, その方がイメージに合うのだ, なんとなく). したがって, 同じ線形代数でも普段見慣れているのとはちょっと見た目が異なることになる(外見が異なるだけで本質は何も変わらない).
以上の準備の下で, 線形符号を用いた情報通信を線形代数の言葉で記述してみよう.
まず,
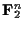 のk次元線形空間Vを考える(k<n). Vは線形符号である.
ここで,
のk次元線形空間Vを考える(k<n). Vは線形符号である.
ここで,
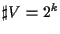 であるから V はkビットの情報を持つ. さて,
であるから V はkビットの情報を持つ. さて,
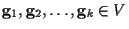 をVの基底とすると,
をVの基底とすると,
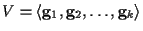 と書けるから, これを使って, 次のように
と書けるから, これを使って, 次のように
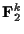 とVとの間の同型写像
とVとの間の同型写像
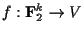 をつくる.
をつくる.
この同型で, 左側の
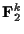 が元のデータの集合で, 右側のVが符号化されたデータの集合, そしてfが符号化を行うしゃぞうである(符号化されたデータの集合がまずあって, それから元のデータの集合が出てくるというのは, 話の順序が逆と思うかも知れないが, これは単に説明の順序の問題であって本質的なことではない. 分かりにくい場合には, まず, 元のデータの集合を
が元のデータの集合で, 右側のVが符号化されたデータの集合, そしてfが符号化を行うしゃぞうである(符号化されたデータの集合がまずあって, それから元のデータの集合が出てくるというのは, 話の順序が逆と思うかも知れないが, これは単に説明の順序の問題であって本質的なことではない. 分かりにくい場合には, まず, 元のデータの集合を
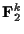 と同一視し(これは前節の話と同様), 次にこれから
と同一視し(これは前節の話と同様), 次にこれから
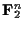 (n>k)への1対1の線形写像を考え, その写像の像(image)Vを符号化したものの集合と考えればよい. 結局のところ,
(n>k)への1対1の線形写像を考え, その写像の像(image)Vを符号化したものの集合と考えればよい. 結局のところ,
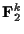 から
から
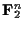 への1対1線形写像を考えることと,
への1対1線形写像を考えることと,
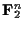 のk次元線形部分空間を考えることとは同じことなのである).
のk次元線形部分空間を考えることとは同じことなのである).
こうすると, 第7節の図における復号化が次の線形写像で与えられることは明らかである.
上の同型写像に現れる行列
を生成行列(generating matrix)と呼ぶ.
符号の誤り訂正能力だけに着目すれば,
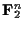 の座標の入れ替えによるCの
取り替えは符号の誤り訂正能力を全く変えない. したがって, 2つの符号CとC'が
の座標の入れ替えによるCの
取り替えは符号の誤り訂正能力を全く変えない. したがって, 2つの符号CとC'が
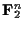 の座標の入れ替えで移り合う場合, 2つを同一視することにする.
の座標の入れ替えで移り合う場合, 2つを同一視することにする.
座標の入れ替えを行ったものを「同一視」することで, 線形符号の生成行列のとり方には, (Cの基底のとり方)+(
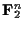 の座標の入れ替え)分の自由度が生じることになる. Cの基底の取り替えと
の座標の入れ替え)分の自由度が生じることになる. Cの基底の取り替えと
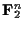 の座標の入れ替えを行うことで, 生成行列は次の形の行列に変形できる.
の座標の入れ替えを行うことで, 生成行列は次の形の行列に変形できる.
上の(Ek P)の形の生成行列を生成行列の標準形(standard form)と呼ぶ.
生成行列の標準形を考えるご利益は次の通りである.
- 1.
- 符号語がデータとパリティ検査ビットにきれいに分かれている.
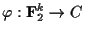 を標準形を生成行列とする線形符号とすると,
を標準形を生成行列とする線形符号とすると,
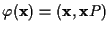 となり, 左のk-ビット
xが元のデータ,
右側の(n-k)-ビット
xPがパリティ検査ビットとなる. したがって,
受信語
となり, 左のk-ビット
xが元のデータ,
右側の(n-k)-ビット
xPがパリティ検査ビットとなる. したがって,
受信語
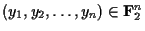 に対してのパリティ検査
(エラーが起きたかどうかのチェック)は,
に対してのパリティ検査
(エラーが起きたかどうかのチェック)は,
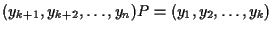 をチェックすればよい.
をチェックすればよい. - 2.
- 復号が簡単.
上のことからすぐわかるように, 復号は, 射影
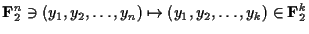 のCへの制限で得られる.
のCへの制限で得られる.
Mitsuru Kawazoe
2001-11-14


![]() のk次元線形空間Vを考える(k<n). Vは線形符号である.
ここで,
のk次元線形空間Vを考える(k<n). Vは線形符号である.
ここで,
![]() であるから V はkビットの情報を持つ. さて,
であるから V はkビットの情報を持つ. さて,
![]() をVの基底とすると,
をVの基底とすると,
![]() と書けるから, これを使って, 次のように
と書けるから, これを使って, 次のように
![]() とVとの間の同型写像
とVとの間の同型写像
![]() をつくる.
をつくる.
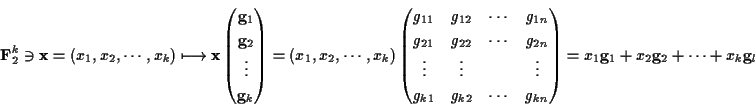
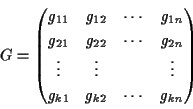
![]() の座標の入れ替えによるCの
取り替えは符号の誤り訂正能力を全く変えない. したがって, 2つの符号CとC'が
の座標の入れ替えによるCの
取り替えは符号の誤り訂正能力を全く変えない. したがって, 2つの符号CとC'が
![]() の座標の入れ替えで移り合う場合, 2つを同一視することにする.
の座標の入れ替えで移り合う場合, 2つを同一視することにする.

![]() の座標の入れ替え)分の自由度が生じることになる. Cの基底の取り替えと
の座標の入れ替え)分の自由度が生じることになる. Cの基底の取り替えと
![]() の座標の入れ替えを行うことで, 生成行列は次の形の行列に変形できる.
の座標の入れ替えを行うことで, 生成行列は次の形の行列に変形できる.